Soal Pilihan ganda

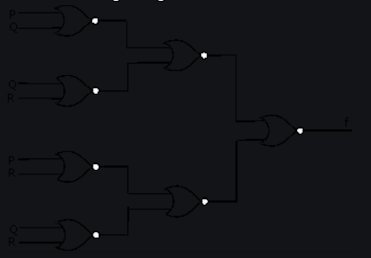
 1. Apa ekspresi Boolean untuk output f dari rangkaian logika kombinasional gerbang NOR yang diberikan di bawah ini?

A. (Q+R)'

B. (P+Q)'

C. (P+R)

D. (P+Q+R)'

Jawaban: A. (Q+R)'

Soal di atas mengandung gerbang NOR. Jika A dan B adalah dua input ke gerbang NOR, gerbang NOR memberikan (A+B)' sebagai output. Misalkan kita berikan nomor ke masing-masing gerbang untuk untuk mempermudah kita dalam menyelesaikannya. 

• Di kolom 1 ada 4 Gerbang NOR, dengan nomor  1 sampai 4 (atas ke bawah). 
• Di kolom ke-2 ada 2 Gerbang NOR, dengan nomor 5 dan 6 (atas ke bawah). 
• Di kolom 3 hanya ada 1 Gerbang NOR, dengan nomor  7.

• Gerbang bernomor 1 memberikan output sebagai: ( P + Q )' 
• Gerbang bernomor 2 memberikan output sebagai: ( Q + R )' 
• Gerbang bernomor 3 memberikan output sebagai: ( P + R )' 
• Gerbang bernomor 4 memberikan output sebagai: ( R + Q )' 
• Gerbang bernomor 5 memberikan output sebagai:

    (( P + Q )' + ( Q + R )')' 

    = ((P + Q)'' . ( Q + R )'') ( hukum De Morgan) 

    = (P + Q ). ( Q + R ) ( Hukum Idempoten, A'' = A) 

    = (PQ + PR + Q + QR ) = 

    (Q(1 + P + R) + PR) = Q + PR ( yang mana, 1 + " apa saja ekspresi boolean" = 1 )

    Demikian pula Gerbang bernomor 6 memberikan output sebagai: 

    R + PQ

                          

     Gerbang bernomor 7 memberikan output sebagai:

    ((Q + PR) + (R + PQ))'

    = (Q( 1+P) + R(1+P))'

    = (Q+R)'

2. Sebuah rangkaian mengeluarkan sebuah digit dalam bentuk 4 bit. 0 diwakili oleh 0000, 1 dengan 0001, ..., 9 dengan 1001. Kombinasional sirkuit dirancang menggunakan 4 bit tersebut sebagai input dan akan memberikan output 1 jika digitnya besar sama 5, dan akan beroutput 0 jika sebaliknya. Jika hanya gerbang AND, OR dan NOT yang dapat digunakan, berapa jumlah minimum gerbang yang diperlukan?

A. 2

B. 3

C. 4

D. 5

Jawaban: B. 3

Kita harus mendapatkan output 1 untuk nilai>=5. kita akan menggunkan tabel kebenaran untuk menyelesaikan soal tersebut

Di sini poin penting adalah bahwa kita perlu membuat pasangan dari 8 elemen menggunakan kondisi don't cares .jadi ekspresi akhirnya adalah

= A+BD+BC

= A+B(C+D) 

Oleh karena itu kita akan menggunakan dua gerbang OR dan satu gerbang AND sehingga total 3 gerbang.